

Start with:į (time between events is < x ) = 1 − e −(1 / MBT) * t) We need to work backwards with the data provided and solve for MBT. What must the new minimum MBT rate be at a minimum to achieve this probability of =<5%? They show a presentation to others in the company that claims the probability of the time until the next failure has been reduced to <5%. In the IMPROVE phase, the team goes on to make several modifications to the machine and collects new data. This is a baseline measurement for the team. The probability of the hemming machine failing in < 150 hours is 73.7% in its current state. To help understand the current state, what is the probability that the time until the next failure is less than 150 hours?į (time between events is < x) = 1 − e −λtį (time between events is < 150) = 1-e -0.008897×150 = 1 - 0.263277 = 0.736723 The Six Sigma team has a goal to increase the MBT to greater than or equal to 150 hours. The time between failures in a hemming machine modeled with the exponential distribution has a MBT rate of 112.4 hours. This is a continuous probability distribution function with formula shown below: time between phone calls at a call center.how long until the next email comes through your Inbox at work.predicting how long a machine will run before unplanned downtime.using the mean time of light bulb, calculate probability of life at specified hours.mean arrival time of planes at an airport.While we all try to read the crystal ball the best we can, predictive modeling can add substance for a decision. All three components of OEE (Availability, Performance, Quality) could benefit from effective probability information.Īn understanding of the probability until a failure or a particular event can be extremely powerful when this information is in the hands of decision makers. When the downtime can be predicted, not only can it control costs but managing labor becomes easier and machine OEE improves. It is a valuable tool to predict the mean time between failures and plays a significant role in Predictive Maintenance, Reliability Engineering, and Overall Equipment Effectiveness (OEE). This distribution uses a constant failure rate (lambda) and is the only distribution with a constant failure rate. Generally, if the probability of an event occurs during a certain time interval is proportional to the length of that time interval, then the time elapsed follows an exponential distribution. If this waiting time is unknown, it can be considered a random variable, x, with an exponential distribution. It's also used for products with constant failure or arrival rates. The Exponential Distribution is continuous distribution commonly used to model waiting times before a given event occurs. “Exponential Distribution lecture slides.” Available online at (accessed June 11, 2013).Share Facebook Twitter Pinterest Exponential Distribution Available online at (accessed June 11, 2013). with mean \lambdaĭata from the United States Census Bureau.ĭata from World Earthquakes, 2013. To do any calculations, you must know m, the decay parameter. X is a continuous random variable since time is measured. The time is known to have an exponential distribution with the average amount of time equal to four minutes. Let X = amount of time (in minutes) a postal clerk spends with his or her customer. Reliability deals with the amount of time a product lasts. The exponential distribution is widely used in the field of reliability.

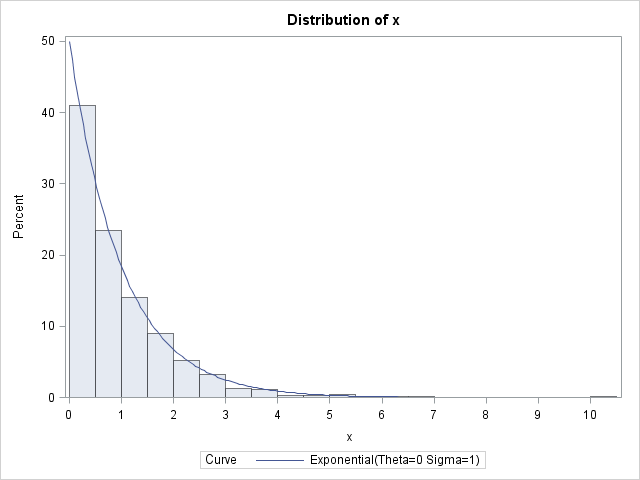
There are more people who spend small amounts of money and fewer people who spend large amounts of money. For example, the amount of money customers spend in one trip to the supermarket follows an exponential distribution. There are fewer large values and more small values. Values for an exponential random variable occur in the following way. It can be shown, too, that the value of the change that you have in your pocket or purse approximately follows an exponential distribution. Other examples include the length, in minutes, of long distance business telephone calls, and the amount of time, in months, a car battery lasts. For example, the amount of time (beginning now) until an earthquake occurs has an exponential distribution. The exponential distribution is often concerned with the amount of time until some specific event occurs. Recognize the exponential probability distribution and apply it appropriately.


 0 kommentar(er)
0 kommentar(er)
